文字列を比較する際の指標の一つに、編集距離があります。具体的には、編集距離とは「一方の文字列をもう一方の文字列に一致させるために必要な $1$ 文字の置換、挿入、削除の最小回数」のことです(後で詳しく説明します)。
生物情報科学(バイオインフォマティクス)において DNA やアミノ酸の配列同士を比較する際にも、編集距離をもとにした指標が使われています。$1$ 塩基の置換、挿入、欠失イベントに対して適切な重み付け*1をした上で編集距離問題を解き、配列を書き並べる(アラインメントと言います)ことは、
- 疾患に特異的な変異を同定する
- 近縁種では配列の相同性が高いことを利用して、系統樹を描く
などに役立ちます。

本記事では、$w$ をワードサイズ、 を文字列長、
をアルファベットサイズとして、
時間の前処理のもと
時間で編集距離を求めるアルゴリズム、その名も Myers' bit-parallel algorithm を紹介します。
本記事は上のような章立てになっています。
1 章で記法、2 章で編集距離について確認したあと、3 章でアルゴリズムの説明を行います。
1 章は読み飛ばしていただいて構いません。それほど突飛なものは出てこないので、後の章を読みながら、分からない記号が出てきた際に戻ってくるのが良いでしょう。
2 章では、編集距離について確認します。3 章で説明するアルゴリズムは 2 章で扱う内容が元になっているので、編集距離をご存じの方も軽く目を通すことをおすすめします。
3 章が本記事のメインディッシュです。天下りに定義→定理→証明→……を与えるのではなく、アルゴリズムを導出していくような構成になっています。
記法
$w$ でワードサイズを表します。ワードサイズはマシンによって異なり、$32$ だったり $64$ だったりします。
文字列は 1-indexed で表します。すなわち、
のとき、$S _ i = c _i~(1 \leq i \leq N)$ です。
$\lor$ で 2 つの整数の bitwise or を表します。例えば、$10010 _ {(2)} \lor 01011 _ {(2)} = 11011 _ {(2)}$ です。
$\land$ で 2 つの整数の bitwise and を表します。例えば、$10010 _ {(2)} \land 01011 _ {(2)} = 00010 _ {(2)}$ です。
$\lnot$ で整数の not を表します。例えば、5 bit 整数においては $\lnot 01011 _ {(2)} = 10100 _ {(2)}$ です。
$\oplus$ で 2 つの整数の bitwise xor を表します。例えば、$10010 _ {(2)} \lor 01011 _ {(2)} = 01001 _ {(2)}$ です。
$a_1 \lor \cdots \lor a_n$ を、$\bigvee _ {k=1} ^ n a _ k$ と表記します。
編集距離
以下のような問題を考えます。
例えば、$S = $ edit, $T = $ dist の場合は、
eを削除する。sを挿入する。
の $2$ 回の操作で $S$ を $T$ に一致させることができます。$1$ 回以下の操作で $S$ を $T$ に一致させることはできないので、$S$ と $T$ の編集距離は $2$ です。
この問題は、以下のような動的計画法で解くことができます。
$d _{i, j} :=(S$ の先頭 $i$ 文字と、$T$ の先頭 $j$ 文字の編集距離$)$ として、
と初期化したのち、
と更新します。ただし、$S_i = T_j$ のとき $\delta(S_i, T_j) = 1$、$S_i \neq T_j$ のとき $\delta(S_i, T_j) = 0$ とします。
先程の例にこのアルゴリズムを適用し、$d$ の表を描いてみると以下のようになります。$d _ {4,4}$ が編集距離と一致していることが確認できますね!

以上のアルゴリズムで、編集距離を $O(NM)$ 時間で求めることができました。
Myers' bit-parallel algorithm
差分を DP する
いよいよ本題です。Myers' bit-parallel algorithm は、一言で言えば「差分を DP する」アルゴリズムです。どういうことでしょうか?
まずは、先程の表をもう一度見てみましょう。

表を眺めてみると、「隣り合うマスに書かれた数の差は、高々 $1$ である」ことに気付きます。実際、以下が成り立つことが知られています。
2. $d_{i, j} - d_{i-1, j-1} \in \{0, 1\}$
1 は上下左右に隣り合うマスについての性質、2 は斜めに隣り合うマスについての性質を述べています。証明は読者の皆様に委ねます。
突然ですが、以下のようなビットベクトル($0, 1$ からなる配列)を考えます。いずれも長さは $N+1$ です。
ただし、$R^ + _ j [0] = R^ - _ j [0] = D^ 0 _ j [0] = 0$ と定義します。
先ほどの例において、$j = 2$ のときの各ビットベクトルは下図のようになります。
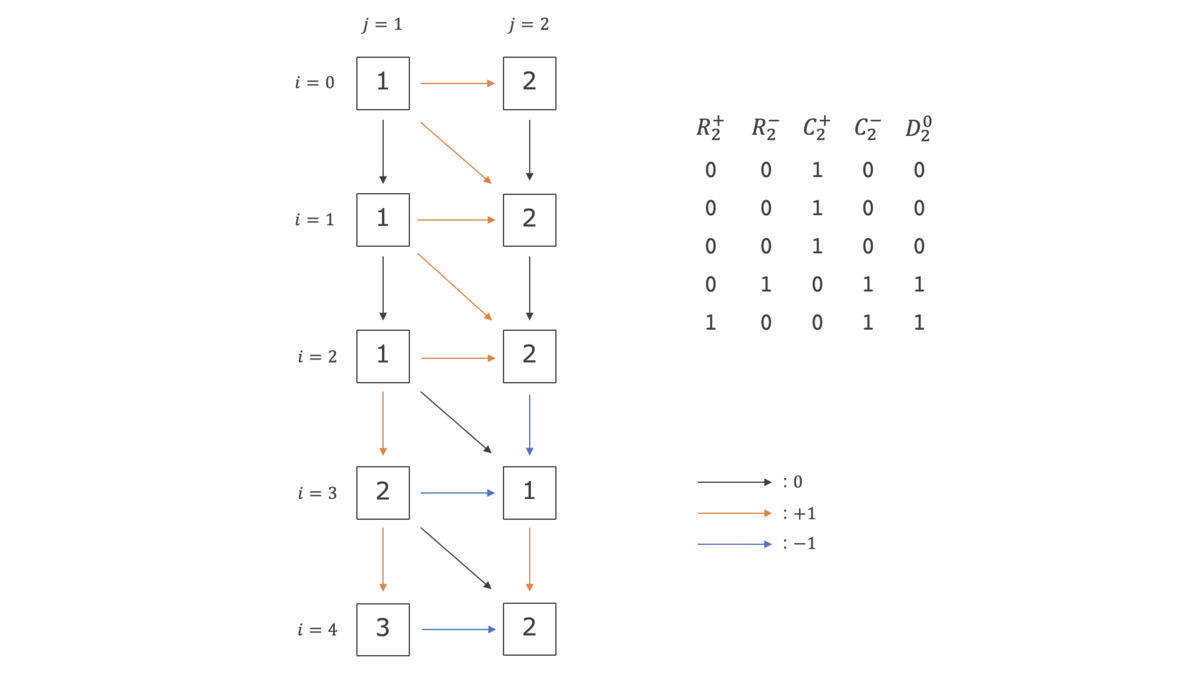
これらのビットベクトルは、元の表と同じだけの情報を持っています。よって、これらを にわたって更新していけば、前章の動的計画法を行ったのと同じといえるでしょう。求めるべき編集距離は、$N + \sum _ {j=1}^ M (C^ + _ j [N] - C^ - _ j [N])$ と表せます(表の最下行の差分を足し上げることで、$d_{N, M}$ を求めています)。さらに、ビット演算を用いて各ビットベクトルを $O(N / w)$ で更新できれば、計算量は全体で $O(NM / w)$ になるだろうという心算です。果たして、そんなに上手くいくのでしょうか?
更新式を作ろう
ひとまず $D^ 0 _ j$ が求まったとして、他の 4 つのビットベクトルの更新式を考えてみましょう。
$C^ - _ j$ の更新式
$i \geq 1$ において $C^ - _ j [i] = 1$ が成り立つのは、以下のような状況に限られます。

よって、$C^ {-} _ {j} [i] = R^ {+} _ {j-1} [i] \land D^ 0 _ j [i]$ が成り立つので、
という更新式が得られました。
$C^-_j [0] = R^ {+} _ {j-1} [0] \land D^ 0 _ j [0] = 0 \land 0 = 0$ となり、$i = 0$ のときも正しく計算できています。
$C^ + _ j$ の更新式
プラスの方はマイナスに比べてやや複雑です。
$i \geq 1$ において $C^ + _ j [i] = 1$ が成り立つのは、以下のいずれかの状況です。

よって、
が成り立ちます。$1$ 行目から $2$ 行目への変形は $R^ {-} _ {j-1} [i] = 1$ ならば $D _ j [i] = 0$ であることから従います。$2$ 行目から $3$ 行目への変形は、短絡評価をイメージすると良いでしょう。
よって、
という更新式が得られました。$C^ {+} _ {j} [0] = 1$ であることも確認できます。
$R^ - _ j$ の更新式
$R$ についても、$C$ と同じような議論ができます。
$i \geq 1$ において $R^ - _ j [i] = 1$ が成り立つのは、以下のような状況に限られます。

よって、$R^ {-} _ {j} [i] = C^ {+} _ {j} [i-1] \land D^ 0 _ j [i]$ が成り立つので、
という更新式が得られました。突然ビットシフトが出てきて面食らうかもしれませんが、これは $i-1$ の情報を $i$ に反映させるために行っているものです。$R^ {-} _ {j} [0] = 0$ であることも確認できます。
注意深い方は「$R^ {-} _ j$ を求めるのに $C^ {+} _ j$ を使っているが、循環が起きていないか?」と不安になったかもしれませんが、前項で $R^ {-} _ j$ を使わずに $C^ {+} _ j$ を求めているので、その心配はありません。
$R^ + _ j$ の更新式
$i \geq 1$ において $R^ + _ j [i] = 1$ が成り立つのは、以下のいずれかの状況です。

よって、
が成り立つので、
という更新式が得られました。$R^ {-} _ {j} [0] = 0$ となっていることも確認できます($\lnot (C^ {+} _ {j-1} << 1)$ ではなく、$\lnot C^ {+} _ {j-1} << 1$ としているところがミソです)。
$D^ 0 _ j$ の更新式 その1
上で求めた 4 つの更新式には、いずれも $D^ 0 _ j$ が登場していました。あとは $D^ 0 _ j$ を求めれば、このアルゴリズムは完成です!
元の動的計画法の漸化式を思い出すと、$D^ 0 _ j [i] = 1$ となる状況には以下の $3$ 通りがあることが分かります。
- $d _ {i, j} = d _ {i-1, j-1} $
このとき、$\delta(S_i, T_j) = 1$ です。
- $d _ {i, j} = d _ {i, j-1} + 1$
このとき、$R^ - _ {j-1} [i] = 1$ です。
- $d _ {i, j} = d _ {i-1, j} + 1$
このとき、$C^ - _ {j} [i-1] = 1$ です。
$\delta$ の代わりに、$I_j [i] = \delta(S_i, T_j), I _ j [0] = 0$ としたビットベクトル $I_j$ を考えると、
という更新式が得られます。めでたしめでたし……?
$D_j$ の更新式 その2
……お気付きの通り、上の式は $D^ 0 _ j [i]$ を求めるのに $C^ - _ j [i]$ を使っており、堂々巡りになっています。これを解消するのが最後にして最大の山場です。
とりあえず $C^ - _ {j} [0] = 0$ であることは分かっているので、$D^ 0 _ {j} [1] = I_j [1] \lor R^ - _ {j-1} [1]$ です。
$i \geq 2$ の場合に、$ C^ - _ {j} [i-1]$ を展開してみましょう。
これを用いて $D^ 0 _ j [2], D^ 0 _ j [3]$ を計算してみると、
同様に、
となります。一般に、
が成り立ちます(証明は数学的帰納法によります)。
$R^ - _ {j-1}$ については後で bitwise or をとることにして、$D' _ j [i] = I _ j [i] \lor \bigvee _ {k=1}^ {i-1} (I _ j [k] \land R^ + _ {j-1} [k] \land \cdots \land R^ + _ {j-1} [i-1])$ について考えてみましょう。
ここからは例を使って説明します(皆様も、ぜひ手を動かしながら追いかけてみてください)。$I _ j [i] \lor \bigvee _ {k=1}^ {i-1} (I _ j [k] \land R^ + _ {j-1} [k] \land \cdots \land R^ + _ {j-1} [i-1])$ を計算するというのは、下図のような操作にあたります。

ここで、$I _ j [i] = 1$ の、$D' _ j $ への寄与を考えます。
- $R^ + _ {j-1} [i] = 0$ のとき
$D' _ j [i]$ のみに寄与します。こちらは、bitwise or で実現できそうです。

- $R^ + _ {j-1} [i] = 1$ のとき
$R^ + _ {j-1}$ における $i$ を含む $1$ の run($1$ が連続している箇所)の右端を $r$ とすると、$D' _ j [i], \ldots, D' _ j [r+1]$ に寄与します。これは、足し算の繰り上がり を使えば表現できそうです。

以上が核となるアイデアです。さらに細部を詰めると、次のようにして $D' _ j$ を得られることが分かります。

- $I _ j \land R^ + _ {j-1}$
$R^ + _ {j-1} [i] = 1$ かつ $I _ j [i] = 0$ をみたすようなビットを消します。$R^ + _ {j-1} [i] = 0$ かつ $I _ j [i] = 1$ である箇所も消滅してしまいますが、④で復活するので大丈夫です。

- $+ R^ + _ {j-1}$
このアルゴリズムのサビに当たる部分です。前述の通り、run の右端へと寄与を伝播します。

- $\oplus R^ + _ {j-1}$
①で消した、$R^ + _ {j-1} [i] = 1$ かつ $I _ j [i] = 0$ をみたすようなビットが②で復活しているので、再び消します。同時に、繰り上がりに巻き込まれて消えてしまったビットを立て直します。このときに run の一部のビットが $0$ になることがありますが、④で復活するので大丈夫です。

- $\lor I _ j$
①や③で消えたビットを復活させます。

以上より、$D^ 0 _ j$ の更新式は
となります。$D^ 0 _ j [0] = 0$ となっていることも確認できます。
全貌
最後に、アルゴリズム全体の擬似コードを載せておきます($I_j$ を前計算するパートは省略しています)。
Input: S, T
Output: S, Tの編集距離
N = |S|
M = |T|
d = N
Rp = 01...1 (1個の0の後ろに、N個の1が連なったビットベクトル)
Rn = 00...0 (N+1個の0 が連なったビットベクトル)
for j = 1 to M:
D0 = ((I & Rp) + Rp ^ Rp) | I | Rn
Cn = Rp & D0
Cp = Rn | ~(Rp & D0)
Rn = (Cp << 1) & D0
Rp = (Cn << 1) | ((~Cp << 1) & ~D0)
d += Cp[N] - Cn[N]
return d
各ビットベクトルを適切なデータ構造(C++ でいう bitset のようなもの*2)で持つことで、for ループ 1 回あたりにかかる時間は $O(N / w)$ となります。また、各アルファベットに対して $I$ を前計算するのに 時間かかります。
おわりに
込み入ったビット演算はよく黒魔術に例えられますが、Myers' bit-parallel algorithm はその極致と言えるかもしれません。 世界には、(ビット演算を使ったものに限らず)魔法のような文字列アルゴリズムが他にも山のように存在します。 本記事を通して皆様が文字列アルゴリズムに興味を持っていただければ、とても嬉しいです。
参考文献
[1] Gene Myers. 1999. A fast bit-vector algorithm for approximate string matching based on dynamic programming. J. ACM 46, 3 (May 1999), 395–415. https://doi.org/10.1145/316542.316550
[2] Mäkinen, V., Belazzougui, D., Cunial, F., & Tomescu, A. (2015). Genome-Scale Algorithm Design: Biological Sequence Analysis in the Era of High-Throughput Sequencing. Cambridge: Cambridge University Press. doi:10.1017/CBO9781139940023